2 menit baca

Tujuan

  1. Menjelaskan pembetulan kesalahan
  2. Menjelaskan cache memori termasuk
  3. Didalamnya adalah fungsi pemetaan

Koreksi Error

Dalam melaksanakan fungsi penyimpanan, memori semikonduktor dimungkinkan mengalami kesalahan. Kesalahan berat biasanya kerusakan fisik memori. Kesalahan ringan yang berhubungan data yang disimpan

Kode Hamming

Diciptakan Richard Hamming di Bell Lab 1950. Mekanismenya menambahkan data word (D) dengan suatu kode, biasanya bit cek paritas (C). Data yang disimpan memiliki panjang D+C

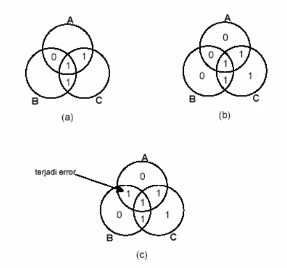
Pasted image 20220323135825.png

Penambahan bit cek paritas untuk koreksi kode Hamming

Data Bits Bit Paritas SEC Bit Paritas DSEC
8 4 5
16 5 6
32 6 7
64 7 8
$2^n, \geq 0$ n + 1 n + 1 + 1

Pasted image 20220323140718.png

Contoh Kasus

Suatu memori internal menyimpan word 8 bit dengan suatu data 00110010 disimpan pada suatu alamat. Hitunglah bit paritas untuk mendeteksi dan memperbaiki kesalahan. Andaikan bit ke-5 mengalam i kesalahan, tunjukkan bagaimana kode Hamming mendeteksi kesalahan tersebut.

XOR = ⊻

Jawab:

Bit Data (D) = 00110010 (8 bit) Bit Paritas (C) = (4 bit)

D + C = 8 + 4 = 12 (12 bit) (12 kolom tabel dibawah)

2^n, n >= 0:

  • 2^0 = 1 (C1) bit paritas ke-1
  • 2^1 = 2 (C2) bit paritas ke-2
  • 2^2 = 4 (C4) bit paritas ke-3
  • 2^3 = 8 (C8) bit paritas ke-4
    0   0 1 1   0 0 1 0
C1 C2 D1 C4 D2 D3 D4 C8 D5 D6 D7 D8
  • C1 = D1 ⊻ D2 ⊻ D4 ⊻ D5 ⊻ D7 = 0 ⊻ 0 ⊻ 1 ⊻ 0 ⊻ 1 = 0
  • C2 = D1 ⊻ D3 ⊻ D4 ⊻ D6 ⊻ D7 = 0 ⊻ 1 ⊻ 1 ⊻ 0 ⊻ 1 = 1
  • C4 = D2 ⊻ D3 ⊻ D4 ⊻ D8 = 0 ⊻ 1 ⊻ 1 ⊻ 0 = 0
  • C8 = D5 ⊻ D6 ⊻ D7 ⊻ D8 = 0 ⊻ 0 ⊻ 1 ⊻ 0 = 1

cara menentukan apa yang di ⊻ kan: mulai dari posisi C-nya ambil sebanyak bit paritasnya langkahi sebanyak bit paritasnya Misal: C1 –> ambil satu langkahi satu, C4 –> ambil 4 langkahi 4

Posisi bit ke 5 dianggap error –> bit D2 maka 0 diganti jadi 1

  • C1 = D1 ⊻ D2 ⊻ D4 ⊻ D5 ⊻ D7 = 0 ⊻ 1 ⊻ 1 ⊻ 0 ⊻ 1 = 1
  • C2 = D1 ⊻ D3 ⊻ D4 ⊻ D6 ⊻ D7 = 0 ⊻ 1 ⊻ 1 ⊻ 0 ⊻ 1 = 1
  • C4 = D2 ⊻ D3 ⊻ D4 ⊻ D8 = 1 ⊻ 1 ⊻ 1 ⊻ 0 = 1
  • C8 = D5 ⊻ D6 ⊻ D7 ⊻ D8 = 0 ⊻ 0 ⊻ 1 ⊻ 0 = 1

Bandingkan bit paritas sebelum dan sesudah error

  • C1 berubah
  • C2 tidak berubah
  • C4 berubah
  • C8 tidak berubah

Poisisi bit error: (jumlahkan yang berubah)

C1 & C4 –> 1 + 4 = 5

Terbukti bit ke 5 terjadi error

Kuis full offline, UTS full online